Abstract
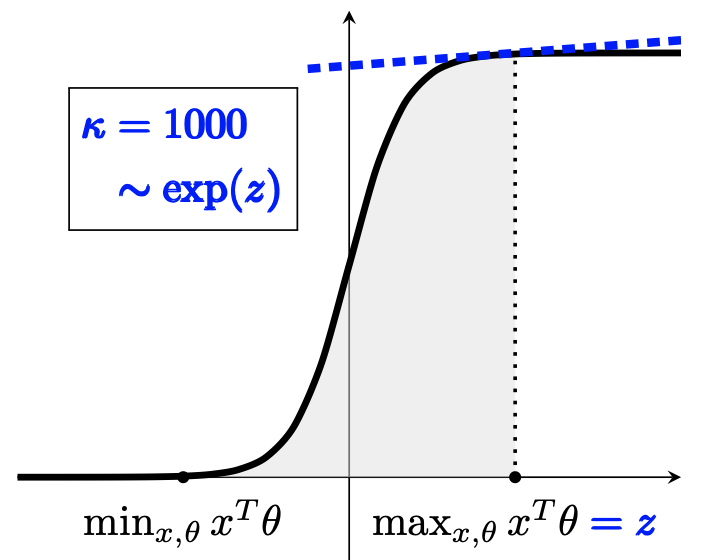
The generalized linear bandit framework has attracted a lot of attention in recent years by extending the well-understood linear setting and allowing to model richer reward structures. It notably covers the logistic model, widely used when rewards are binary. For logistic bandits, the frequentist regret guarantees of existing algorithms are \(\tilde{\mathcal{O}}(\kappa \sqrt{T})\), where \(\kappa\) is a problem-dependent constant. Unfortunately, \(\kappa\) can be arbitrarily large as it scales exponentially with the size of the decision set. This may lead to significantly loose regret bounds and poor empirical performance. In this work, we study the logistic bandit with a focus on the prohibitive dependencies introduced by \(\kappa\). We propose a new optimistic algorithm based on a finer examination of the non-linearities of the reward function. We show that it enjoys a \(\tilde{\mathcal{O}}(\sqrt{T})\) regret with no dependency in \(\kappa\), but for a second order term. Our analysis is based on a new tail-inequality for self-normalized martingales, of independent interest.