Abstract
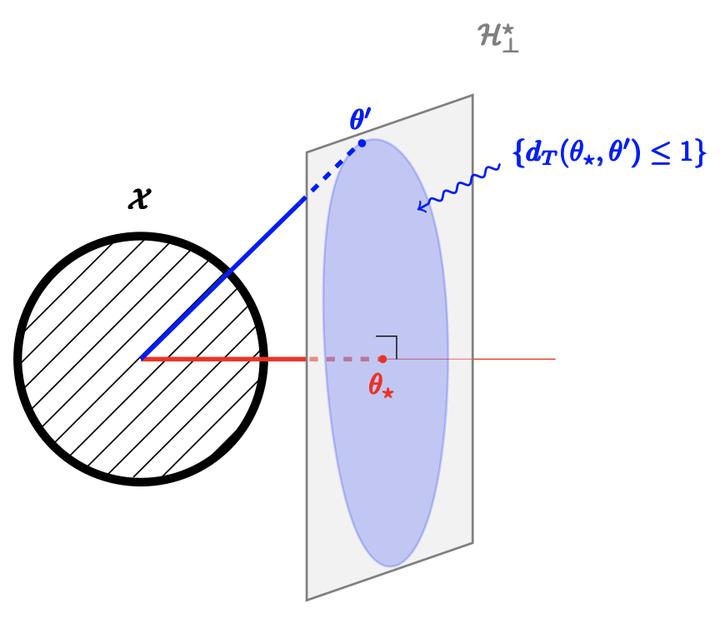
Logistic Bandits have recently attracted substantial attention, by providing an uncluttered yet challenging framework for understanding the impact of non-linearity in parametrized bandits. It was shown by \cite{faury2020improved} that the learning-theoretic difficulties of Logistic Bandits can be embodied by a \emph{large} (sometimes prohibitively) problem-dependent constant $\kappa$, characterizing the magnitude of the reward’s non-linearity. In this paper we introduce a novel algorithm for which we provide a refined analysis. This allows for a better characterization of the effect of non-linearity and yields improved problem-dependent guarantees. In most favorable cases this leads to a regret upper-bound scaling as $\tilde{\mathcal{O}}(d\sqrt{T/\kappa})$, which dramatically improves over the $\tilde{\mathcal{O}}(d\sqrt{T}+\kappa)$ state-of-the-art guarantees. We prove that this rate is \emph{minimax-optimal} by deriving a $\Omega(d\sqrt{T/\kappa})$ problem-dependent lower-bound. Our analysis identifies two regimes (permanent and transitory) of the regret, which ultimately re-conciliates \citep{faury2020improved} with the Bayesian approach of \cite{dong2019performance}. In contrast to previous works, we find that in the permanent regime non-linearity can dramatically ease the exploration-exploitation trade-off. While it also impacts the length of the transitory phase in a problem-dependent fashion, we show that this impact is mild in most reasonable configurations.